Kunci Jawaban
Kunci Jawaban Matematika Kelas 8 Halaman 11, 12, Gunakan Teorema Pythagoras untuk Menentukan Nilai
Kunci Jawaban Matematika Kelas 8 Halaman 11, 12 Ayo Kita Berlatih 6.1. Ini merupakan pembahasan yang terdapat dalam buku Matematika Kelas 8 Bab 6 Te
Penulis: Mona TR | Editor: Mona Triana
TRIBUNPADANG.COM - Kunci Jawaban Matematika Kelas 8 Halaman 11, 12 Ayo Kita Berlatih 6.1.
Ini merupakan pembahasan yang terdapat dalam buku Matematika Kelas 8 Bab 6 Teorema Pythagoras.
Soal terdiri dari esaai nomor 1, 2, 3, 4, 5. Kunci Jawaban ini ditujukan sebagai panduan bagi para siswa dalam mengerjakan tugas di rumah.
Diharapkan para siswa mampu menyelesaikan tugas yang telag diberikan.
Baca juga: Kunci Jawaban Matematika Kelas 11 Halaman 85 Uji Kompetensi 9.1 Semester 2
Kunci Jawaban Matematika Kelas 8 Halaman 11, 12 Ayo Kita Berlatih 6.1
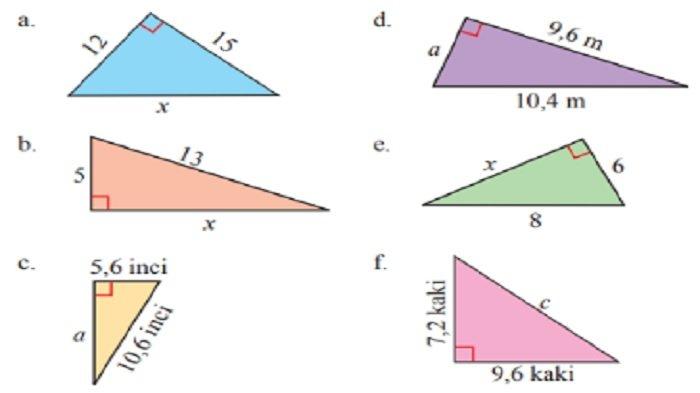
1. Gunakan teorema Pythagoras untuk menentukan nilai yang belum diketahui pada masing-masing gambar berikut.

Jawaban :
a)
x = √(122 + 152)
= √(144 + 225)
= √369
b)
x = √(132 - 52)
= √(169 - 25)
= √144
= 12
c)
a = √(10,62 - 5,62)
= √(112,36 - 31,36)
= √81
= 9 inchi
d)
a = √(10,42 - 9,62)
= √(108,16 - 92,16)
= √16
= 4 m
e)
x = √(82 - 62)
= √(64 - 36)
= √28
f)
a = √(7,22 + 9,62)
= √(51,84 + 92,16)
= √144
= 12 kaki
2. Tujuan dipasangkan kawat bubut pada suatu tiang telepon adalah untuk menopangnya. Kawat bubut dipasang pada tiang telepon setinggi 8 meter dari tanah.
a. Jelaskan cara yang akan kalian lakukan untuk menentukan panjang kawat bubut tanpa mengukur langsung kawat tersebut.
b. Tentukan panjang kawat jika jarak antara kawat dan tiang pada tanah adalah 6 meter
Jawaban :
a) Caranya dengan mengukur jarak antara kawat dengan tiang lalu, Dengan menggunakan rumus Teorema Pythagoras kita dapat mencari panjang kawat bubut,
b)
kawat = √(jarak2 + tinggi2)
= √(62 + 82)
= √(36 + 64)
= √100
= 10 m
Jadi, panjang kawat bubut tersebut adalah 10 meter.
3. Tentukan nilai x pada kedua gambar berikut.

Jawaban :
Bangun I )
x = √(Sisi miring2 - Sisi tegak2)
= √(202 - 122)
= √(400 - 144)
= √256
= 16 cm
Jadi, panjang x adalah 16 cm.
Bangun II )
Cari nilai y terlebih dahulu,
y = √(132 - 52)
= √(169 - 25)
= √144
= 12 mm
x = √(y2 + 352)
= √(122 + 352)
= √(144 + 1225)
= √1369
= 37 mm
Jadi, panjang x adalah 37 mm.
4. Apakah suatu segitiga yang panjang ketiga sisinya berturut-turut 9 cm,12 cm, dan 18 cm merupakan segitiga siku-siku? Jelaskan.
Jawaban :
Kita dapat menggunakan Teorema Pythagoras, dengan rumus :
sisi paling panjang kuadrat = sisi 1 lainnya kuadrat + sisi 2 lainnya kuadrat
182 = 92 + 122
324 = 81 + 144
324 = 225 (salah)
Jadi, jawabannya adalah salah karena tidak memenuhi kriteria Teorema Pythagoras.
5. Jika panjang sisi-sisi suatu segitiga siku-siku berturut-turut adalah x, 15, dan x + 5, tentukan nilai x.
Jawaban :
Dengan menggunakan pythagoras maka,
x⊃2; + 15⊃2; = (x + 5)⊃2;
x⊃2; + 225 = x⊃2; + 10x + 25
x⊃2; - x⊃2; - 10x = 25 - 225
-10x = -200
x = -200 / -10
x = 20
Jadi, nilai x adalah 20.
Baca juga: Kunci Jawaban Matematika Kelas 9: Tentukan Panjang dari Unsur Tabung yang Ditanyakan
Baca juga: Kunci Jawaban Matematika Kelas 9: Manakah Belah Ketupat di Bawah Ini yang Kongruen? Jelaskan
Disclaimer:
- Kunci Jawaban Matematika ini hanya sebagai bahan referensi dalam menjawab pertanyaan dan bukan acuan utama
- Kunci Jawaban Matematika ini mungkin akan berbeda dengan pembahasan yang diberikan guru sekolah
- TribunPadang.com tidak bertanggung jawab terhadap kesalahan dalam kunci jawaban ini
Kunci Jawaban Matematika Kelas 8
Kunci Jawaban Matematika
Kunci Jawaban
Matematika
Bab 6 Teorema Pythagoras
| Kunci Jawaban Bahasa Indonesia Kelas 8 Halaman 204 Kegiatan 8.1 Bagian A, Materi Drama Lengkap |

|
|---|
| Bahasa Indonesia Kelas 8 Halaman 224 Kegiatan 8.8: Kunci Jawaban Cerpen Kena Batunya |

|
|---|
| Kunci Jawaban Bahasa Indonesia Kelas 11 Halaman 207: Analisis Isi Resensi dalam Format Tabel |

|
|---|
| Kunci Jawaban Bahasa Indonesia Kelas 7 Halaman 170 Semester 2, Soal Kata Berima Lengkap |

|
|---|
| 55 Contoh Soal Bahasa Indonesia Materi Majas dan Kunci Jawaban Lengkap untuk Latihan Siswa |

|
|---|















Isi komentar sepenuhnya adalah tanggung jawab pengguna dan diatur dalam UU ITE.